Accelerationcentripetal is a property present in bodies that describe a circular motion. It is a Vector greatness that points to the center of the trajectory, moreover, its module is directly proportional to the square of the velocity of the body and inversely proportional to the radius of the curve.
See too: Uniform circular motion: concept and mind map
What is centripetal acceleration?
Centripetal acceleration is represented by a vectorpointing towards the center of a circular path. Because it is a acceleration, your unit of measure is the m/s², however, unlike the average acceleration and from instantaneous acceleration, centripetal acceleration is not characterized as a variation of speed, but rather as a variation in the direction and direction of speed.
The centripetal acceleration vector is tangent to the trajectory of the body, moreover, it is perpendicular to the direction of velocityclimb, also called velocitytangential.

Even in cases where a mobile describes a circular and uniform movement, that is, with a constant angular velocity, there is centripetal acceleration, therefore, every movement that occurs on circular paths is accelerated.
Centripetal acceleration is directlyproportional to the tangential velocity of the mobile, squared, and inverselyproportionalto the radius of the curve, as we will show below.
Do not stop now... There's more after the advertising ;)
Centrifugal acceleration
Centrifugal acceleration is a concepterroneous very used. Since, when placed in rotation, objects tend to “run away from the center”, we imagine the existence of a centrifugal acceleration, however, such acceleration does not exist. In fact, what exists is the inertia of objects moving in circular paths.
THE inertia it is the tendency of a body to remain in its state of rectilinear movement, with constant velocity, or at rest. centripetal force, which points to the center. At that moment, its inertia causes the centrifugal movement to occur.
See too: Newton's First Law – what is it, examples and exercises
Centripetal acceleration of the Earth
The Earth performs a movement of translation, at an average distance of 150 million kilometers, moving at about 100,000 km/h. Also, in the equator line, a speed of rotation from the earth is about 1600 km/h.
Even moving so quickly, we are not able to perceive the centripetal acceleration of the Earth, because the accelerations produced by the rotation and translation movements are thousands of times weakerthat the very gravity terrestrial.
However, it is known that the centripetal acceleration of the Earth plays a very important role: it makes the seas occupy the Equator, if the planet stopped rotating, they would leave the region and migrate towards the North and South.
See more: Is it true that water flows in different directions according to each hemisphere?
Centripetal Acceleration Formula
there is more than one formula used to calculate centripetal acceleration, know each one:
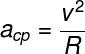
v - velocity
R – radius of the curve
In addition to this, there is a centripetal acceleration formula that can be calculated in terms of the velocityangular, ω, note:
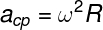
v - velocity
R – radius of the curve
Centripetal force and centripetal acceleration
Just like the force resulting from translational movements, the centripetal force is the resultant force that acts on a body, causing it to rotate. Therefore, this quantity is equivalent to the mass of the body multiplied by the centripetal acceleration. Therefore, centripetal force and centripetal acceleration are different things, since the centripetal force is defined by the product of mass and centripetal acceleration.
Exercises on centripetal acceleration
Question 1) A 1000 kg vehicle moves at 20 m/s on a circular path with a radius equal to 40 m. Check the alternative that indicates the centripetal acceleration submitted to the vehicle.
a) 5 m/s²
b) 1 m/s²
c) 10 m/s²
d) 8 m/s²
e) 4 m/s²
Template: Letter C
Resolution:
Let's make use of the acceleration formula that relates velocity to the radius of the trajectory, check it out:

According to the calculation performed, the centripetal acceleration that the car underwent was 10 m/s², thus, the correct alternative is the letter c.
Question 2) A race car driver enters a high-speed curve, undergoing a centripetal acceleration of 15 m/s². Knowing that the radius of the turn is 60 m, determine the magnitude of the angular velocity of the racing car in the turn.
a) 3.0 rad/s
b) 2.5 rad/s
c) 0.5 rad/s
d) 0.2 rad/s
e) 1.5 rad/s
Template: Letter C
Resolution:
Let's calculate the angular velocity using the centripetal acceleration formula below, here's how:

According to the above calculation, the vehicle changes its direction by about 0.5 radian every second. According to the definition of radians, this equates to about 28° every second, so the correct alternative is the letter c.
Question 3) Determine the centripetal acceleration of an object moving on a circular path with a radius equal to 4 m, taking into account that this object completes one revolution every 4 s. (Use π = 3.14).
a) 9.8 m/s²
b) 8.7 m/s²
c) 0.5 m/s²
d) 6.0 m/s²
e) 2.5 m/s²
Template: Letter a
Resolution:
To calculate the centripetal acceleration of the object, it is necessary to know the magnitude of its scalar velocity, or even its angular velocity, in that sense, let's get this second velocity. To do this, we must remember that each complete revolution is equivalent to sweeping an angle equal to 2π rad, and that it takes 4 s:

Based on the obtained result, we find that the centripetal acceleration that keeps the object on a circular path is approximately 9.8 m/s², so the correct alternative is the letter a.
By Rafael Hellerbrock
Physics teacher